# Triple Integrals in Cylindrical Coordinates

## Cylindrical Coordinates

Recall that polar coordinates use a radius and angle $(r,\theta)$ to represent a coordinate in space. Each pair of numbers corresponds to only one point.

We can extend this similarly to cylindrical coordinates, where instead of using $(x,y,z)$, we use a radius, angle, and height. In this case, $P_{xy}$, the point on the xy-plane corresponding to $(x,y,z)$, can be represented in polar coordinates as $(r,\theta)$. Therefore, we can show the 3-D point by adding a z-value as height: $(r,\theta,z)$.

This grouping also uniquely describes point $(x,y,z)$, so it is a valid representation.

![Cylindrical Coordinate Example](cylindrical.jpeg)

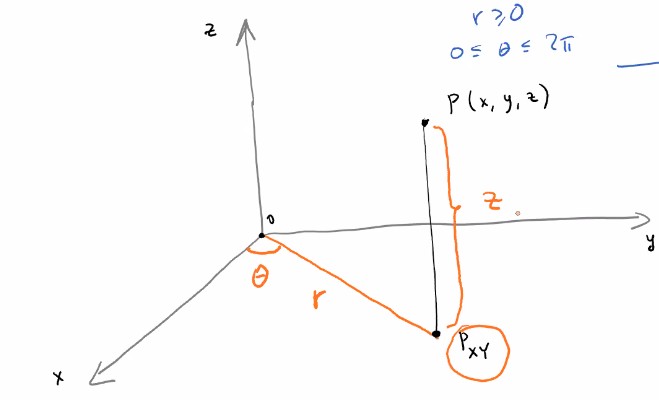
To convert from one to the other, we can use the trigonometric equations for normal polar coordinates and leave $z$ the same.

$$P = (x,y,z) \cong (\sqrt{x^2 + y^2}, \arctan(y/x), z) = (r,\theta, z)$$
$$P = (r,\theta, z) \cong (r\cos(\theta), r\sin(\theta), z) = (x,y,z)$$

So, what if we used cylindrical coordinates to do a triple integral?

To answer this, we need to know what the analog of polar rectangles is for cylindrical coordinates (a polar rectangular prism):

$$R = \{(r,\theta,z)|\alpha\le\theta\le\beta, a\le r\le b, c\le z\le d\} = [a,b]\times[\alpha,\beta]\times[c,d]$$

![A polar rect prism](polar_rect_prism.jpeg)

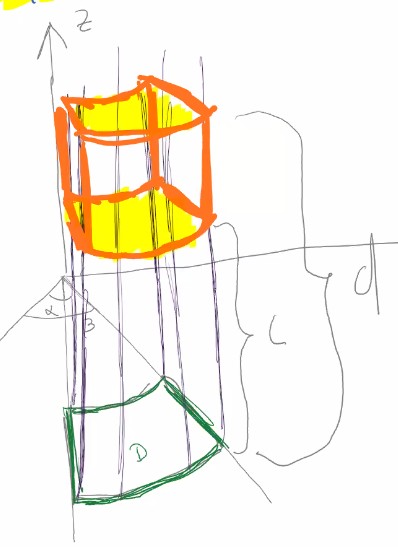
This simply extends the polar rectangle into cylindrical coordinates by adding a range in $z$

## Triple Integrals in Cylindrical Coordinates

So we are taking an integral over this volume:

$$\iiint\limits_E f(x,y,z)dV = \iint\limits_D\left(\int_c^d f(x,y,z)dz\right)dxdy$$

Which we can represent in cylindrical coordinates (note that $f$ is multiplied by $r$, as with polar integrals):

$$\int\limits_\alpha^\beta\int\limits_a^b\int\limits_c^d f(r\cos(\theta), r\sin(\theta), z)r\ dzdrd\theta$$

These limits can also be represented by a function, as with other types of multiple integrals. This allows the domain to be distorted in two of the 3 coordinates:

$$E = \{(r,\theta,z)|\alpha\le\theta\le\beta, h_1(\theta)\le r\le h_2(\theta), g_1(x,y)\le z\le g_2(x,y)\}$$

$$\int\limits_\alpha^\beta\int\limits_{h_1(r)}^{h_2(r)}\int\limits_{g_1(x,y)}^{g_2(x,y)} f(r\cos(\theta), r\sin(\theta), z)r\ dzdrd\theta$$

or

$$\int\limits_\alpha^\beta\int\limits_{h_1(r)}^{h_2(r)}\int\limits_{g_1(r\cos(\theta),r\sin(\theta))}^{g_2(r\cos(\theta),r\sin(\theta))} f(r\cos(\theta), r\sin(\theta), z)r\ dzdrd\theta$$

<details>
  <summary>Click to show explanation</summary>

We can do this by inputting each part:

$$\iiint\limits_E f(x,y,z)dV = \iint\limits_D\left(\int_{g_1(x,y)}^{g_2(x,y)} f(x,y,z)dz\right)dxdy$$

We can then abstract the inner portion as another function,

$$G(x,y) = \int_{g_1(x,y)}^{g_2(x,y)} f(x,y,z)dz$$

Now we can insert it into a normal polar integral:

$$\iint\limits_R G(x,y) = \int\limits_\alpha^\beta \int\limits_{h_1(\theta)}^{h_2(\theta)} G(r\cos(\theta), r\sin(\theta)) r\ drd\theta $$

So we can evaluate the whole:

$$\int\limits_\alpha^\beta\int\limits_{h_1(r)}^{h_2(r)}\int\limits_{g_1(r\cos(\theta),r\sin(\theta))}^{g_2(r\cos(\theta),r\sin(\theta))} f(r\cos(\theta), r\sin(\theta), z)r\ dzdrd\theta$$

</details>

<!-- Not sure about the following -->
<!-- This would also work for a distortion of $\theta$ and $r$ or $\theta$ and $z$. Keep in mind that the boundaries of the first integral will be a function of the remaining variables -->

<details>
  <summary>Click to show Exercise 25 (Sec 15.8)</summary>

### Question

Find the volume of the solid $E$ that lies between the paraboloid [$z = 24 - x^2 - y^2$](https://llumen.neocities.org/projects/ray-grapher.html?eq=z%3D24-x%5E2-y%5E2&zoom=40&m=[-154,-50]) and the cone [$z = 2\sqrt{x^2 + y^2}$](https://llumen.neocities.org/projects/ray-grapher.html?eq=z%5E2%3Dx%5E2%2By%5E2&zoom=40&m=[-54,-10])

#### Solution
We can find the volume by simply integrating over $1$

$$Volume\ of\ E = \iiint\limits_E 1 dV$$

These two equations will look like [this](https://llumen.neocities.org/projects/ray-grapher.html?eq=(24-x%5E2-y%5E2-z)(x%5E2%2By%5E2-z%5E2)&zoom=40&m=[-154,-50]):

![The volume](domains_cyl_1.jpeg)

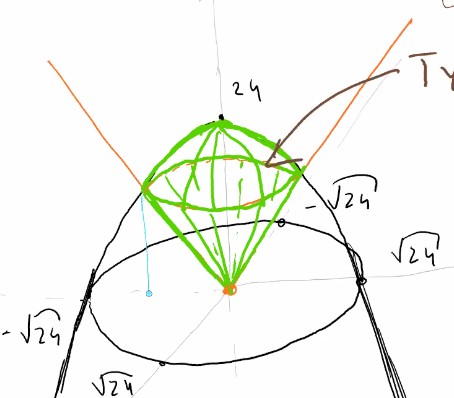
We can find the location where the functions intersect by solving the system of z:

$$
\begin{cases}
  z = 24 - x^2 - y^2 \\
  z = 2\sqrt{x^2 + y^2}
\end{cases}
= 
x^2 + y^2 = 4^2
$$

So since $r^2 = x^2 + y^2$, we can find that r goes from $0$ to $4$. We also know it is a full circle, so the angle is from $0$ to $2\pi$.

So let's set up the integral:

$$\iint\limits_D\int\limits_{2\sqrt{x^2 + y^2}}^{24 - x^2 - y^2} 1\ dV = \int\limits_0^{2\pi}\int\limits_0^4\int\limits_{2\sqrt{x^2 + y^2}}^{24 - x^2 - y^2} r\ dzdrd\theta$$

Which we can simplify to (using $r^2 = x^2 + y^2$):

$$\int\limits_0^{2\pi}\int\limits_0^4\int\limits_{2r}^{24 - r^2} r\ dzdrd\theta$$

This can now be evaluated.

</details>

<script src="/source/texme.js"></script>
<link rel="stylesheet" href="/source/theme.css">